Rymddiagonal

Filmad genomgång, klicka här

Att byta volymenheter

Mål:

• Kunna uttrycka samma volym i olika enheter
• Kunna förklara hur litersystemet är uppbyggt
• Kunna förklara och utföra enhetsomvandlingar mellan de olika systemen.

Filmklipp som visar enhetsomvandling i litersystemet.

Filmklipp som visar hur kubikdecimeter kan omvandlas till kubikcentimeter 

Filmklipp som visar enhetsomvandling mellan t.ex millilter och kubikcentimeter

Uppgifter att arbeta med i boken:

• s.58-59 blå kurs
• s.48-49 grön kurs
• s.66-67 röd kurs

Paruppgift: Arbeta i par eller i mindre grupp. Gör diagnos s.56 uppgift 1-6 muntligt. 

Ge mig feedback på hur diagnosen gick. Vad behöver vi kanske arbeta mer med?

Filmad genomgång

TESTUPPGIFT ( Hämtad från NP 2008 )

Chokladmousse ska serveras i glas som
är 5 cm höga och har en diameter på 6 cm.
När Hanna är klar med smeten har hon
2 liter mousse. Får all Hannas mousse
plats i 15 glas? Motivera din slutsats
med resonemang och beräkningar.

Filmad genomgång

E: Kan beräkna volymen på glaset

C: Korrekta beräkningar men felaktiga slutsatser. Redovisning möjliga att följa.

A: Kan utifrån beräkningar på volymen av glaset använda effektiva metoder för att beräkna om 15 glas räcker. Korrekta enheter, beräkningar och slutsatser. Redovisningen är lätt att följa.

Räknat exempel om koppartråd. Uppgift 43

E: Kan med hjälp av miniräknare beräkna basytan hos koppartråden

C: Kan till stor del utföra volymberäkningen av koppartråden och använda enheter på ett korrekt sätt.
Redovisningen är möjlig att följa.

A: Kan med effektiva metoder utföra beräkningar där man utförligt redovisar och har ett korrekt
resonemang. Hanterar enhetsbyten med mycket stor säkerhet.

Rätblockets, Cylinderns och Prismats volym


Mål

• Kunna beräkna volymen 
• Kunna ange volymen i olika volymenheter
• Kunna redogöra för begreppen basyta och höjd

Uppgifter 

• s.60-62 Blå kurs
• s.46-47 och s.50-51 Grön kurs
• s.66-67 Röd kurs

Par/Gruppuppgift

Vilka mått kan  en Coca-cola burk ha ?

• Strategier/metoder ( Vad behöver ni veta? Hur ska vi räkna?)
• Resonemang ( Varför vet vi att det stämmer? )
• Redovisning ( Hur förklarar vi ? )

  

Uppgift från NP

Sidan i en liksidig triangel är 5 dm. Hur stor area
har triangeln? Ett av alternativen är rätt. Ringa in
ditt svar.                                                                                                                              (0/1)

         6,3 dm²                 10,8 dm²                 12,5 dm²                

                      15 dm²                  25 dm²   

Svar : 10,8 dm2

Hur litersystemet och metersystemet hänger ihop i volymberäkningar



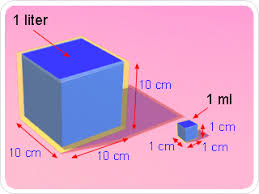
Bilden visar oss hur litersystemet och metersystemet används inom volymberäkningar

Viktigt att inse och komma ihåg är:

• En kubikcentimeter har samma volym som en milliliter
• En kubikdecimeter har samma volym som en liter
• Det får plats 1000 st kubikcentimeter ( milliliter )  i en kubikdecimeter (1 liter )

Problemlösning

Den här uppgiften cirkulerar på nätet och är inlämnad av en elev. Hur hänger uppgiften ihop?

Volymenheter

Det finns två enheter som används när man uttrycker volym.

När man beräknar volym kan man utgå från metersystemet vilket ger oss volymer som kubikmeter osv.

Man kan också utgå från litersystemet och det ger oss volymer som deciliter osv.

Det finns alltså två olika system för volymberäkning.

• Varför finns det olika system att beräkna volym?
• Finns det några kopplingar mellan systemen?

Litersystemet

• Vi använder prefix framför enheten liter för att uttrycka delar av en liter.
• Prefixen som används är deci ( tiondel ), centi ( hundradel ) och milli ( tusendel )

Vi använder positionssystemet för att förstå t.ex  hur många ml går det på en cl.
Metoden är att börja "fylla upp" tusendelspositionen ( milli ) med en tusendel i taget tills vi behöver använda hundradelspositionen.

Om vi förstår hur vi kan använda positionssystemet så kan vi skriva en egen "fusklappp" om hur volymenheterna förhåller sig till varandra.

1. Hur många ml går det på en cl
2. Hur många ml går det på en dl
3. Hur många ml går det på en liter

Uttryck 150 ml på olika sätt, hur många hittar ni?

Vi arbetar med arbetsblad 2:6

14 November:

Vi började även med arbetsblad 2:7

Problemlösning

  

På ett idrottsgymnasium spelar 1/2 av eleverna innebandy och 1/2 spelar fotboll.
Hur stor del av eleverna spelar både innebandy och fotboll?


På ett idrottsgymnasium spelar 2/3 av eleverna innebandy och 3/4 spelar fotboll.
Hur stor del av eleverna spelar både innebandy och fotboll?

Minst 5/12 av eleverna spelar både innebandy och fotboll.

Som mest spelar 8/12 av eleverna både innebandy och fotboll.