Arbetsplan för kap 3 Geometri

v.48 Utvärdering, genomgång av prov och taluppfattning/huvudräkning

v.49 Symmetri och Likformighet

v.50 Skala

v.51 Kvadrater och kvadratrötter

v.2 Repetition. Taluppfattning/Huvudräkning.

v.3 Pythagoras

v.4 Matematikprov måndag

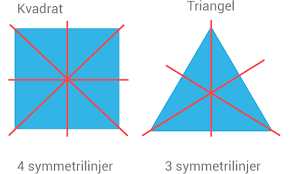
Symmetri

Vi går igenom begreppen spegelsymmetri och rotationssymmetri.

Ni ska få börja med att rita symmetriska figurer. Klicka på länken Webövningar, Matteva ( Klicka på Geometri )

Användbara länkar:
Webmatte.se Klicka här!

NCM ( Nationellt centrum för matematik )

Matematikvideo, symmetrilinjer

Webövningar, Matteva ( Klicka på Geometri )

     


Testa dina kunskaper om symmetri, klicka här !

Arbete i boken s.111-113

Taluppfattning och huvudräkning

Vi arbetar med uppgifterna på sidan 119.

Uppföljning av provresultat

Ni ska få rätta " Gottfrids prov " och ge motiveringar till varför ni ger poäng eller inte.

Bidra med era tankar kring hur Gottfrid har tänkt och vilka tips ni vill ge honom.

Antal poäng per uppgift ser ni på tavlan.

1. Gå igenom provet och gör egna markeringar
2. Samtala parvis eller i mindre grupper. Vad har Gottfrid gjort bra och vad kan han utveckla? 
3. Gemensam diskussion

Nytt Quiz att öva på inför provet

Länk till frågorna, klicka här !

Lycka till!

Utvärdering av perioden

Vi närmar oss slutet av den här perioden. Nu är det dags att utvärdera vårat arbete.

Tre frågor att fundera kring ( skriv på en lapp anonymt )

1. Hur tycker ni att det  " nya upplägget är " ?
2. Hur har inlärningen varit? ( eget arbete och lektionsupplägg av läraren )
3. Förslag på förbättringar.

Filmade uppgifter från diagnosen

Proportion. Hur saker förhåller sig till varandra.

Elis, Stig och Gunvor har köpt en lott och vunnit 900 kr

Lotten kostade 240 kr.

Elis satsade 40 kr

Stig betalade 140 kr

Gunvor satsade 60 kr.

Hur ska vinsten fördelas?

Diagnos inför provet

Länk till diagnosen, klicka här !

Filmade genomgångar " Taluppfattning och huvudräkning "

Läxa till torsdag

                                       

                                       

                                       

                                       

Diagnos inför provet

Diagnos inför provet. Klicka på länken!

Varför kunna matematik ?

Inspirerande intervju med Farid Nolen., klicka på länken !

Taluppfattning och huvudräkning

Vi arbetar med taluppfattning och huvudräkning.

s.81. Hemuppgift göra färdigt till på torsdag. Filmade genomgångar ska publiceras här.

Procent och ekvationer

Vi arbetar tillsammans med exempel från sidan 82

Vi kompletterar med att rita bilder.

Vi jobbar med vågskålar för att göra det mer greppbart.

Uppgifterna går att lösa utan ekvationslösning.

Kritisk aspekt: 28 % av x skrivs som 0,28x

Ekvationslösning

Arbeta med räkneexempel på sidan 78.

På vilka olika sätt kan man lösa uppgiften ?

Redovisa era olika lösningar.

Gör en egen liknande uppgift.

Ekvationslösning

Ekvationslösning är en effektiv problemlösningsmetod.

Tänket inom ekvationslösning är att hålla saker i balans.

Likhetstecknet är viktigt.

Du måste göra lika på båda sidor om likhetstecknet för att hålla ekvationen i balans.

Kontrollera ditt svar genom prövning.



En kvadrat har 12 cm längre omkrets än en liksidig triangel.

Triangelns sidor är två cm längre än kvadratens.

Beräkna kvadratens area.

Börja med att rita figurer.

Teckna uttryck för sidorna i figurerna.

Teckna uttryck för figurernas omkrets.

4X - 3 ( X + 2 ) = 12

4X - ( 3X + 6 ) = 12

4X - 3X - 6 = 12

X - 6 = 12

X = 18

Prövning:

4 x 18 - 3 ( 18 + 2 )  = 12   ????????


4 ( y -5 ) = 8

X/5    +  8 = 10

5X + 2 = 3X + 8

Uppgift 2072 b) gemensamt